1. What is Problem Solving?
sequence of operators를 찾는것.
- 에펠탑 그림그리는거에 비유하면, 빈도화지는 initial state, 에펠탑은 goal state가 된다.
Example: Traveling Salesperson Problem

가능한 모든 solution을 다 나열하면 n!가 되는데, 이는 효율성에 문제가 생긴다.


The Turing test
- 사람이 생각하는 형태처럼 기계로 solution을 찾아가면 문제를 해결할 수 있지 않을까?
문제 푸는 방식의 체계화
1) Initial (start) state
2) Operators (successor functions) - state를 변경시키는 액션
- 1)과 2)가 state space를 구성.
3) Goal test - 최종목적에 도달했는지 테스트
4) Path cost - Operator를 취할때마다 걸리는 cost. (TSP같은 경우는 거리.)
Solution은 initial에서 goal로 가는 path가 되며, 최종적으로 원하는건 path cost가 가장 낮은 solution!
2. Example Problems

States - 9개 사각형중 8개타일의 위치
Operators - 빈칸의 left, right, up, down 움직임
Goal test - goal configuration과 match시
Path cost - step당 1 cost
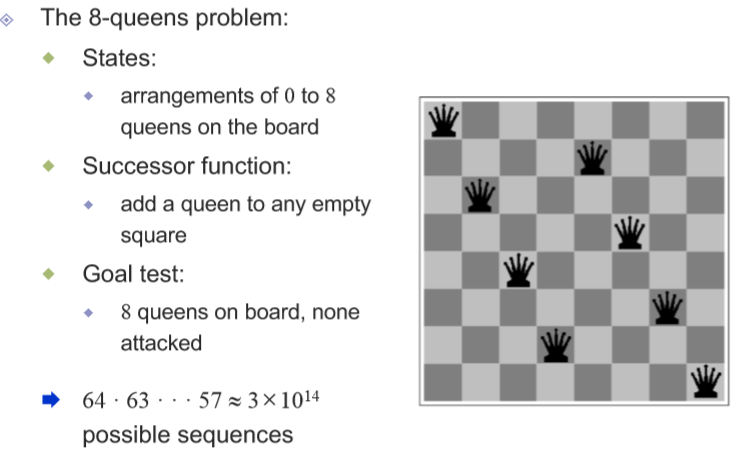
A better formulation
- 1 row에 1 queen만 add해도 state space가 줄어든다
- 하지만 n이 커지면, 여전히 모든 경우의 수를 세기엔 많음


3. Searching for Solutions
1) initial state로 시작하는 search tree를 형성한다.
- branch는 다른 state로가는 operator와 cost가 된다.
- 각 node는 각 state가 된다.
2) 현재 state에서 operator를 적용한다. (state를 expanding)
- 원래 node는 parent가 되고, expanded된 node는 child가 됨.
- leaf node는 현재 노드에서 다음 액션을 취했을 때 갈 수 있는 노드가 됨.
- leaf node의 집합을 frontier 혹은 open list라고 한다. (search상에서 다음으로 갈 수 있는 노드들의 집합)
(frontier는 expanded될 수 있는 것들의 집합.)
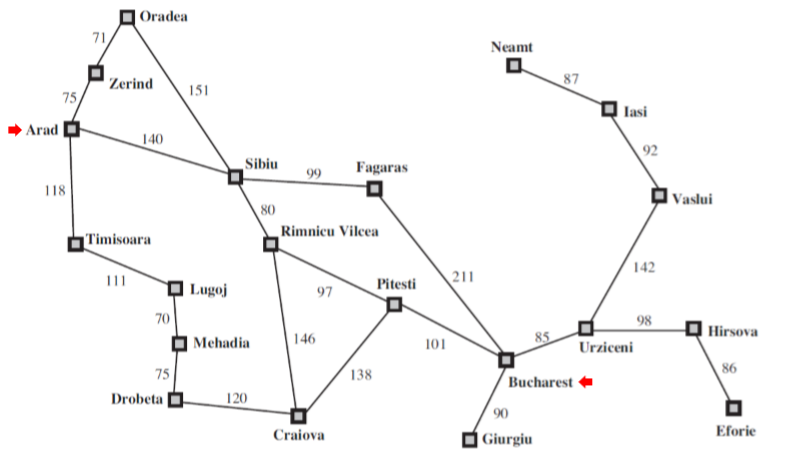
Arad에서 Bucharest를 가는 경우를 생각해보자.
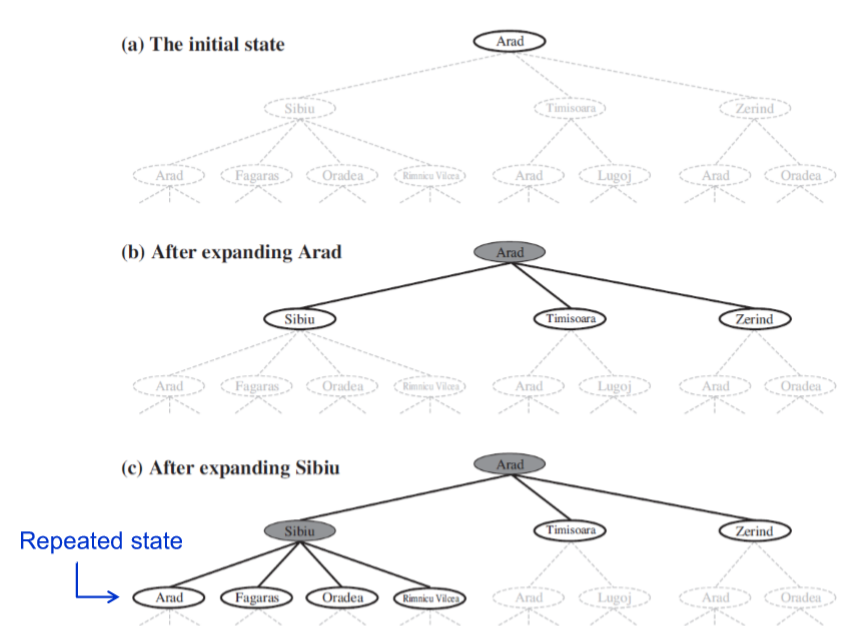
(b) arad에서 expand한 상태, 다음으로 갈 수있는 frontier에는 sibiu timisoara zerind가 있음.
(c) sibiu에서 expand한 상태, 다음으로 갈 수 있는 frontier에는 arad, fagaras, oradea, rimicicu vilcea.
-> 여기서 arad를 또 가면 repeated state가 발생.
위처럼 모든 패턴을 구하는게 tree search이다.

- tree search는 현재를 기준으로 갈수 있는 곳을 다 가본다.
- frontier가 empty인경우는 끝. goal이 아니라면 solution을 못찾았으니까.
- leaf node를 어떻게 설정하느냐?가 search strategy임.
단점
- tree search를 하게 되면, repeated state가 생길수있어서, loop가 생길 수 있다.
- reduncant path -> 같은 path를 또 만들수있다.
왜냐하면, 모든 경우를 다 찾아가고, 과거에 어디를 expand했는지 고려x, 매번 현재를 기준으로
다음 취할 수 있는 액션만 expand하기 때문에. (과거 무시)
-> 그러면 과거에 expand했던 노드를 방문했다고 체크하면 되겠다.
-> Graph-Search 알고리즘. (expand했던 노드는frontier에서 빼줌.)
-> tree와 graph의 차이는 explored set의 유무!


dead end가 되는 상황은 tree든 graph든 모두 생길수있음.
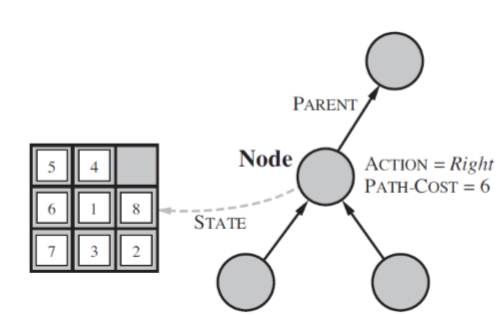
한 노드는 4가지 컴포넌트로 구성된다.
1) 현재 state
2) 도달하기전 parent
3) 어떤 action으로 왔는지? (위의 경우 Right)
4) 지금까지 몇번옮겼느냐? (Path-Cost)

- optimal은 path-cost가 minimal한걸로 take
- solution은 이런 action들의 sequence가 된다. ( parent찾아서 root까지 쫓아가면 처음 root부터 시퀀스까지 연결하면 솔루션이 된다.)

- frontier에는 queue형식으로 넣어준다.
- explored set는 빨리 찾아야되기때문에 (효율) hash table로 구성.
평가 기준
- completeness : 솔루션을 찾도록 보장하느냐?
- optimality : optimal한 solution을 찾느냐?
- time complexity : 시간 복잡도가 낮을수록 좋음.
- space complexity : 메모리 고려
4. Uninformed Search Strategies
Unimformed search (blind search)
- 현재 상태에서 goal까지 path cost 혹은 step의 수에대한 정보가 없는 경우
Informed search (heuristic search)
- 어떤 state가 promising한지 알 수 있음.
- 더욱 효율적.
1) Breadth-first search
frontier에서 expand되지 않은 노드중 가장 shallow한 노드를 expand.
frontier는 FIFO queue 방식.
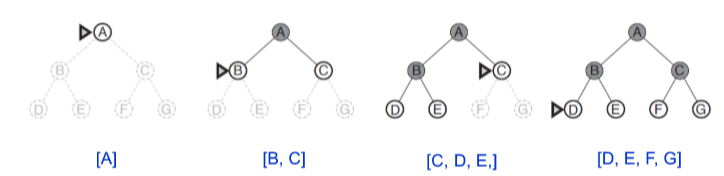

평가
- Complete and optimal
- Time & memory complexity


2) Uniform-cost search
shallowest 노드 대신에, cost가 적게드는 노드로 expand한다!
Frontier는 우선순위 큐 (path cost에 의한)
단점 - zero-cost action의 무한 sequence가 존재하다면, infinite loop에 빠질 수 있음!



- A로부터 생성된 chlid node B가 C와같은 STATE인 경우,
Path-Cost (C) < Path-Cost(B)이므로 B를 제거할 수 있음.
평가

3) Depth-first Search
fontier에서 가장 deep한 node를 expand한다.
(frontier는 stack!)
새로운 state가 parent들중과 같을경우 discard한다. (infinite loop를 피하기 위해서)
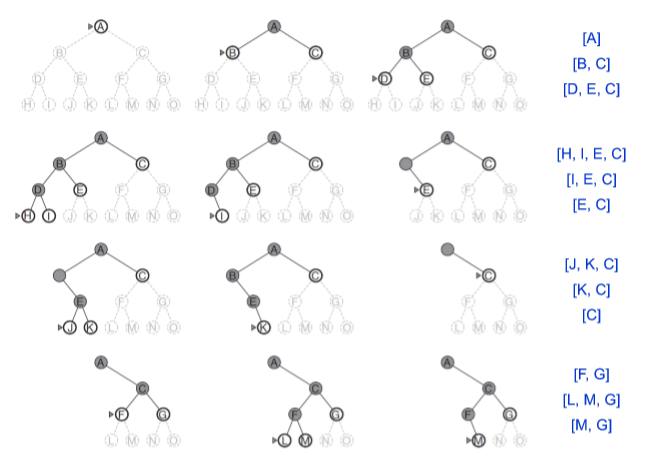
평가
- Modest memory requiremetns: O(bm) (b: branching factor, m:maximum depth)
- Takes O(b^m) time
- infinite-depth spaces에서는 complete, oprimal하지 않다!
- finite spaces에서는 Complete
- finite spaces에서는 Not optimal (redundant paths때문에)
4) Depth - limited Search
DFS의 단점
- complete하지 못하다.
- solution을 찾아도 oprimal한지 장담못함.
-> limit를 두자!
- depth의 형태를 어느정도안다고 했을 때, diameter를 잡아주자.
- time과 space는 DFS보다 좋게 할 수 있지만, 그와 마찬가지로 complete, optimal하지 않는 경우가 생길 수 있음.
(limit을 작게 잡으면 solution을 못찾으니까 complete하지 않을수가 있음.)
- l>=d가 아니면 complete도 optimal도 아니다. (하지만 limit을 사전에 알기는 어려움.)

- 위의 수도코드를 보면, limit까지만 내려가고 돌아옴.
- limit를 정한 DFS라고 생각하면 됨.
5) Iterative Deeepening Search
limit를 모르기때문에, 계속해서 반복적으로 하나씩 증가시키면서 적용하는 방식
Graph-Search-based implementation은 meaningless
-> 노드가 커지면, explored set이 기하급수적으로 커져서, 저장해둔다해도 의미가 없음.
-> depth기반의 search는 implementation할때는 tree based라고 생각하면 됨.
평가
- optimal도 찾고, complete도 한다.


- complete하고 optimal한 모습
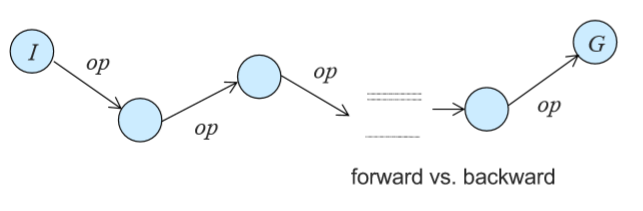
6) Bidrectional Search
Goal node에서 거꾸로 initial로 찾아오는 방식.

문제점
- goal node에서 시작하여, 이전 노드를 연속적으로 생성해야한다. (이전 노드들 계산의 어려움.)
- goal state가 여러개 있는 경우
- goal state에 대한 설명(조건)만 있다면? (체스에서 checkmate의 경우.)
- 각 새 노드가 나머지 절반에 표시되는지 여부를 효율적으로 확인할 수 있는 방법 필요
- 각 절반에 어떤 검색 전략을 할것인가?
5. Comparing Uninformed Search Strategies

- biderectional은 bfs방식.
6. Tree Search vs. Graph Search

'4학년 1학기 수업 > 머신러닝 및 응용' 카테고리의 다른 글
| [머신러닝 및 응용] CH.2 Informed Search and Exploration (0) | 2020.05.07 |
|---|
