[컴퓨터 비전개론] CH.1 Image Filtering

1. 이미지란?

Intensity values를 사용하여 매트릭스 혹은 격자의 형태로 표현.

2. 이미지 특성

이미지는 제한된 수만큼 픽셀을 보유한다.

픽셀 값

- grayscale은 0~255.

- 컬러는 RGB같은 경우, 각 채널당 0~255까지 각 1바이트로 총 3바이트로 표현 가능.

수학적 함수로 표현하면, 

 

3. 이미지 변환

수학적인 함수를 이용해서 operator를 적용하면, 이미지 변환을 얻을 수 있음.

밝기에 대한 이미지 변환, 미러링의 변환

오늘날, 특별한 종류의 operator에는 convolution이 있다.

대표적으로 노이즈제거하는데 이용.

 

4. 왜 이미지는 노이즈를 가지는가?

이미지 획득하는 과정

카메라 자체 문제 (Dead pixels)

인화 단계 문제

 

5. 노이즈 제거

가장 그럴싸한 방법은 제일 근사한 값들이 비슷한 컬러를 가질 가능성이 크므로, 주변값을 보는 것.

현재 픽셀을 주변 픽셀들과 평균을 내서 대치를 하게 되면 조금더 원래값에 가까이 가지 않을까?

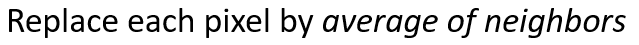
- 위에서 설명한 방법이 다음처럼 계산하는 Mean filtering

 

왼쪽부터 전체 이미지에 대해서, 박스 필터를 적용

- Mean filtering을 적용하면, 노이즈들이 제거되고, 디테일 부분은 블러링으로 사라진다.

6. 필터

필터링 - 새로운 이미지를 만드는 것.

왜 필요한가?

- 새로운 유용한 정보를 얻기 위해서 (edges나 contours (shape이해를 위한) )

- 이미지 enhance (노이즈 제거를 위한 블러링, enhance image를 위한 sharpen 등)

- Convolutional Neural Networks의 key operator

 

7. Linear filtering

가장 간단한 필터링으로 cross-correlation, convolution이 있음.

- 주변 값의 weighted sum으로 픽셀의 대체할 값을 찾는다.

그 값을 찾아내기 위해서 매트릭스를 주게 되는데 이를 Kernal 혹은 mask 혹은 filter라고 함.

8. Mean filtering

주변의 평균으로 pixel값을 대체

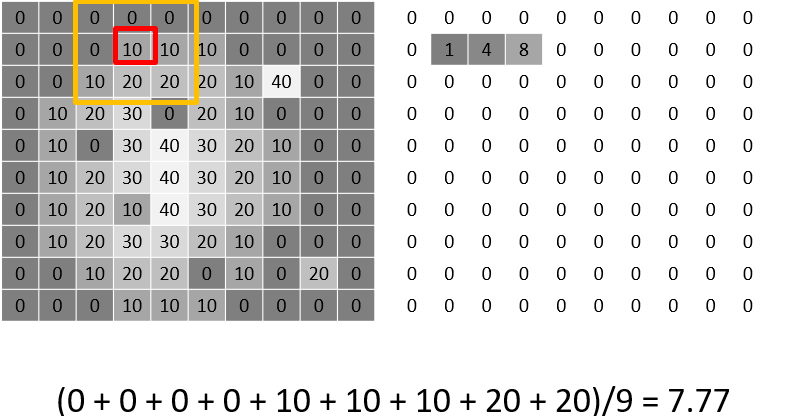
9. A more general version

정확한 Linear filtering의 수식이 된다.

위 그림에서 general시켜보면, 이와 같은 수식이 나온다.

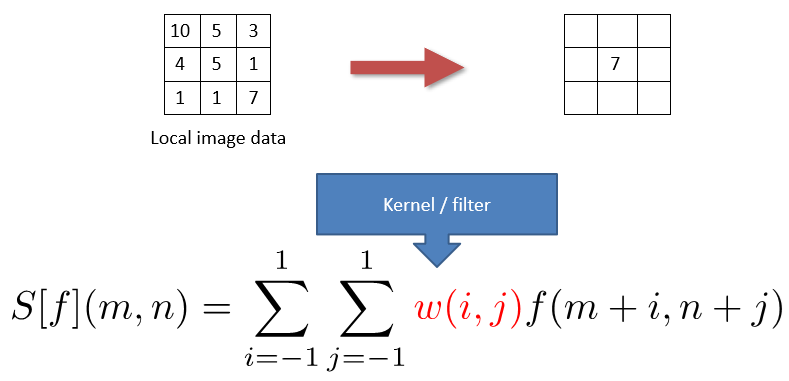
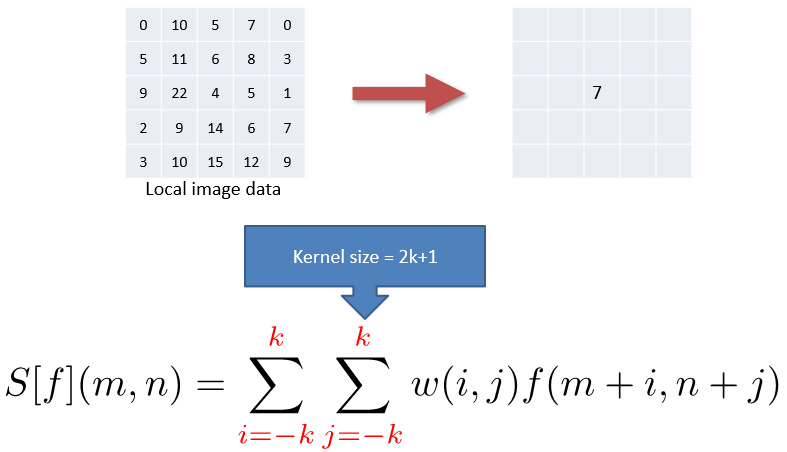
최종적으로, 수식은 다음과 같이 정리가 가능하다.

10. Convolution과 cross-correlation

Cross correlation

- 수식

위와 같이, 해당하는 값끼리 계산

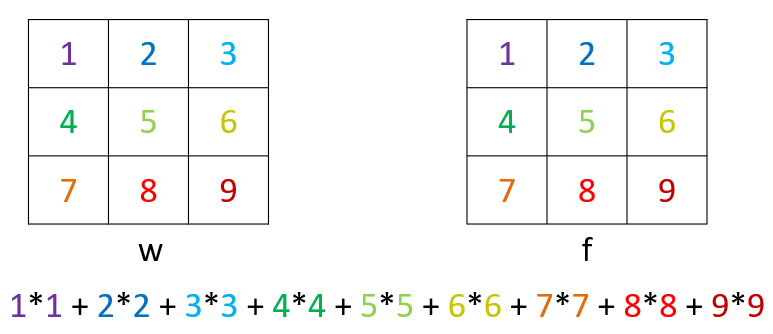
Convolution

- 수식

위와 같이, 대칭시켜서 계산

- Convolution은 좌우 아래위로 바뀌기때문에 커널자체를 바꾸는 것도 방법이다.

아래위로 미러링하고, 좌우로 미러링하면 다음과 같이 새로운 커널이 되고, Convolution 효과를 낼 수 있다.

11. 특징 : 선형성

 

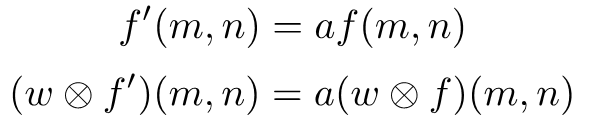
12. 특징 : Shift invariance

선형적으로 이동했을 때, convolution도 Shift가 된다.

그래서, shift를 하고 convolution을 하던지 순서 상관이 없음.

13. Filters: examples

Kernel의 주변값은 0이고 가운데만 1이므로 픽셀값은 변화가 없음.

- Linear filters: examples

- Mean filters: examples

커널 자체가 좌우아래위로 대칭이라서, convolution해도 달라지는건 없기 때문에, 블러링.

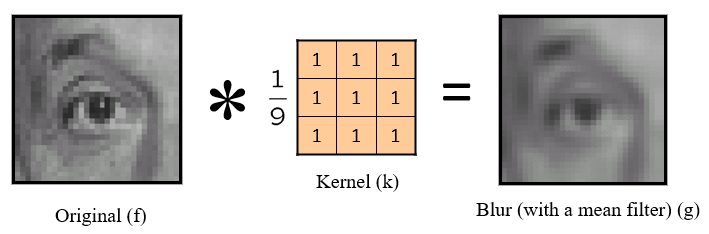
14. Sharpening

어떤 필터를 써야 이 효과를 가질 수 있는가?

-> 블러링 이미지는 오리지널에서 디테일이 없다는 특징을 이용!

오리지널 - 블러링 = 디테일

오리지널 + 디테일 = 샤프닝

- 수식

- Sharpening filter

15. Gaussian filter

Mean filter - 모든 픽셀들이 같은 가중치를 가짐.

Gaussian filter - 주변의 픽셀들이 멀리있는 픽셀보다 관련성이 높다, 가까운 픽셀에 더 많은 가중치!

0이 되는 지접에 피크값으 가지게 된다. 중심 픽셀에서 가중치가 멀어질수록, 표준편차를 통해서 구한다.

값은 중요치 않고, Sum이 1이 되도록 normalize해야함.

감마가 0.5라면, 미세한 블러링 효과. 중심에 밀접해있는 커널.         1이라면, 중심에서 좀더 완만하게 구성되므로 조금더 블러링이 됨.   3이라면, 주변의 픽셀을 비슷한 가중치로 적용해서 심한 블러링.

Gaussian filter는 디테일한 부분(High-frequency)을 없애게 된다.

따라서, low-pass filter라고도 부른다.

 

16. Sharpening revisited

오리지널 - (low-pass 필터) = High-pass 필터

오리지널 + α(High-pass 필터) = Sharpening Image

 

17. Convolution이 중요한 이유?

1) Shift invariance때문에. -> 시프트가 된다하여도, convolution에는 영향이 없다.

2) Linearity때문에. -> 인풋이 변하게될 때 우리가 예상할 수 있는 방향으로 간다.

18. Non-linear filter

선형성이 아닌 대표적인 예시.

대표적인게 Thresholding 필터

Rectification

- 함수가 주어지면, 양수만 출력한다.

Mean filtering

- Speckle noise는 평균값이 굉장히 달라져서 Mean filtering 사용 못함.

(Median filter는 평균값이 아니라, 중간값이므로, 사용 가능!)

 

18. 요약

2가지 일반적인 기법

- convolution과 cross-correlation

특징

- Shift-invariant과 Linearity

Smoothing과 Sharpening에 사용되는 필터

- Low-pass filter과 high-pass filter

CNNs의 주요 요소가 된다!